What Is an Intracluster Correlation Coefficient? Crucial Concepts for Primary Care Researchers

INTRODUCTION

Clustered samples are not as statistically efficient as simple random samples. Similarities among subjects in clusters can reduce the variability of responses from a cluster compared with those expected from a simple random sample. If statistics meant for simple random samples are used to design and analyze clustered studies, they will result in overestimation of the effective sample size. This issue is important for primary care research, because the design of many primary care research studies creates clusters.

This article will use a case study to introduce the concepts involved in cluster sampling. It is intended as an introduction to the concepts and language of cluster sampling; researchers are encouraged to consult a statistician familiar with cluster sampling to help in the design and analysis phases of clustered studies. The goal is to raise the awareness of cluster sampling issues among primary care researchers and to help primary care researchers design and publish statistically rigorous findings.

DEFINITION AND EXPLANATION OF CLUSTERED DESIGNS

Case Study

A clinical trial was designed to evaluate the impact of physician advice on condom use. The outcome was patient-reported use of condoms 6 months after randomization to a control group or a counseling group. The investigator avoided contamination by randomizing the physicians to be control physicians or counseling physicians (randomizing at the physician level) but wanted to analyze data at the patient level. Four physicians in solo practice were recruited; 2 to counsel, and 2 to be controls. A sample-size calculation was done, which suggested that for a 2-sample t test, a minimum effect size of 0.5, and a significance level of .05, 128 patients total would be necessary to achieve a power of 80%. Each physician was therefore asked to recruit 32 patients. When the paper was submitted to a journal, the paper was rejected for “erroneous statistics” and “inadequate power: 61%.”

What happened? Most statistical methodologies were designed to analyze data that is both selected and analyzed on the same level. Clustered data result when some preexisting group structure is used to select study participants, but the researcher is interested in the individual level data. Clustered designs can be used for many reasons, but they always cause some loss of statistical efficiency as a result of the “relatedness” within the preexisting groups. Primary care research, which often studies patients from multiple private practices, can produce clustered results by selecting groups of patients at the practice (or practitioner) level, then analyzing the data at the individual patient level, as in our case study.

Why does clustering erode statistical power? Consider the nature of preexisting groups. Most groups form because of some kind of selection factors. Among patients who all see the same primary care physician, there can be many similarities that may include geographic, socioeconomic, racial, ethnic, sexual, religious, political, or age-related similarities, stemming from the propensity of patients to choose a physician with whom they identify. All of these factors can have some impact on the average response of one physician’s patients compared with another’s.

The responses of persons selected by any or all of the factors mentioned above tend to be more similar to one another’s than the responses of a group of individuals selected truly at random. Because these responses are similar, they lead to a decrease in the variation among responses of persons in the same cluster, or the variance of the within-cluster responses. This similarity among responses within a group can magnify the apparent differences in outcomes or responses between groups, and they must be taken into account. Adjustment for clustering thus results in a reduction of the effective sample size.

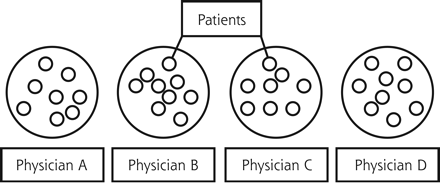
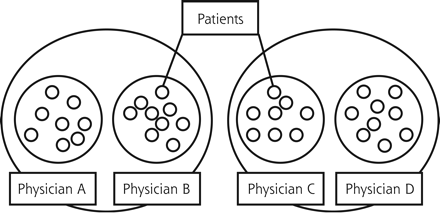
In the case study, solo practitioners were chosen at the physician level to keep the discussion simple. Figure 1⇓ illustrates the design of the study. Physicians who choose to work together, however, share similarities just as their patients do, and these similarities must be taken into account. Using physicians who worked together would have introduced a third level, the practice level, to our study. This concept is illustrated in Figure 2⇓. Multilevel clustering is termed nesting, and there are specific statistics to deal with that mathematical situation. Clustering is a specific term for the simplest type of nesting, using only 2 levels of data, as shown in Figure 1⇓.

• Download figure
• Open in new tab
• Download powerpoint

Figure 1.

Two-level nesting, or clustering.

• Download figure
• Open in new tab
• Download powerpoint

Figure 2.

Three-level nesting.

ADVANTAGES AND DISADVANTAGES OF CLUSTERED DESIGNS

While the loss of statistical efficiency and the need to recruit more study participants are clear disadvantages of clustered studies, there are some advantages to clustering. Clustering is often used for practical reasons when a simple random sample would be unrealistic. For example, a random survey of all patients in a given area would be extremely difficult. A clustered survey of randomly chosen patients within primary care practices is much more practical.

Clustering is the design of choice to avoid a phenomenon known as contamination. In our example, asking the same physician to present 2 entirely different counseling scripts to his or her patients is impractical; the physician will likely get confused. Also, patients of the same physician may be acquainted. Some patients could pass on a version of the counseling to other patients. As a result, the loss of efficiency from clustering is necessary to preserve the integrity of the intervention.

THE INTRACLUSTER CORRELATION COEFFICIENT, OR ρ

The intracluster correlation coefficient (ICC) ,or ρ (the Greek rho), is a measure of the relatedness of clustered data. It accounts for the relatedness of clustered data by comparing the variance within clusters with the variance between clusters. Mathematically, it is the between-cluster variability divided by the sum of the within-cluster and between-cluster variabilities.

Equation 1: *

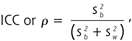
where s_b² = the variance between clusters, and s_w² = the variance within clusters.

Values of ρ range from 0 to 1 in human studies. From equation 1, as the within-cluster variance (s_w²) moves toward 0, ρ gets closer and closer to 1. In the theoretical case where ρ = 1, all responses within a cluster are identical. In that case the effective sample size is reduced to the number of clusters.

A very small value for ρ implies that the within-cluster variance is much greater than the between-cluster variance, and a ρ of 0 shows that there is no correlation of responses within a cluster. Usually, values of r are between 0.01 and 0.02 in human studies.^2–,⁴ The calculation of ρ usually requires a pilot study. We encourage all investigators to publish their ρ values, which will (eventually) aid in being able to estimate ρ for a given type of population.

EFFECTIVE SAMPLE SIZE AND THE DESIGN EFFECT

In accounting for the similarities among clustered subjects, there is a net loss of independent data. The effective sample size is the term used to describe the sample size in clustered samples compared with the number of subjects actually enrolled in the study. For example, if you have 4 physicians’ offices (from the case study above) enrolling 32 patients each, you have 128 subjects in your study. Depending on the intracluster correlation coefficient and the design effect, however, you may effectively have far fewer subjects enrolled in your trial from a statistical perspective.

To get the effective sample size, the total sample size (the number of patients per cluster times the number of clusters) is divided by a correction factor that includes ρ and the sample size per cluster (m). This correction factor is called the design effect. In the case study above, we created the special case of clustered data with all groups having the same number of subjects (each physician recruited 32 patients). In this special case:

Equation 2:

and Equation 3:

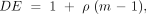
where m = number of subjects in a cluster, k = number of clusters, mk = total number of subjects in a clustered study, ESS = effective sample size, DE = design effect, and ρ = intracluster correlation coefficient (see equation 1).

If ρ = 0, then the design effect = 1, and the sample size is unaffected. If ρ > 0, even if it is still very small, the design effect may be magnified by a large cluster size (m). This would then reduce the effective sample size of the study (see equation 2). If ρ = 1, the design effect (equation 2) is 1, and the effective sample size therefore reduces to k, the number of clusters.

These equations can be reversed in the planning phase to calculate correctly the total sample size needed for a clustered study. All power calculations and resultant sample size estimates can be calculated initially using usual formulas for a clustered study, which will give researchers the effective sample size. Equation 2 can be used to find mk, or the total required sample size, given the effective sample size and design effect

THE EFFECT OF ρ AND THE DESIGN EFFECT ON POWER AND SAMPLE SIZE CALCULATIONS

To illustrate the effect of ρ and the design effect on sample size and power, we will do a sample calculation. Using our case study, we have 4 physicians recruiting 32 patients each. Let us say that ρ = 0.017 in this case. What is the effective sample size after adjusting for clustering?

If m = 32, k = 4, and ρ = 0.017:

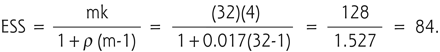
Note that despite the small value for ρ, the design effect came out to 1.527. This reduced our effective sample size to 84 compared with the 128 subjects actually enrolled in the trial, which explains why the power was only 61%.

If we change the numbers for m and k, we can show that the magnitude of the design effect is highly dependent on m, the number of patients in a cluster. Table 1⇓ illustrates the changes in effective sample size and power for our example as we vary m and k but hold the product mk constant. Table 2⇓ shows the effect of increasing m while holding k constant. Note the increasing design effect as m increases and its effect on the effective sample size; the investigator would have needed to recruit almost 80 patients per physician (320 total subjects) to adequately power his study with only 4 physicians. Table 3⇓ shows that by increasing the number of physicians he enrolled in his study to 16, he would only have needed a total of 160 subjects to reach 80% power.

SUMMARY

The intracluster correlation coefficient, or ρ, is a measure of relatedness of responses within a cluster. In human studies it is usually small, but in the design effect it is magnified by the number of elements in the cluster (m). The smaller the design effect, the larger the effective sample size. A high k (number of clusters) and a low m (number of elements within a cluster) give the smallest design effect. When designing studies, increasing clusters (k) will increase the study’s power more than increasing the elements in the clusters (m). Standard formulas can be used to calculate sample sizes in clustered situations, but the resulting effective sample size (ESS) must then be adjusted using the design effect (DE) to find the total required sample size.